1.8 Electromagnetic Rock Properties
In their seminal paper on the electromagnetic behavior of rocks, Fuller and Ward (1970) discussed the expectation that the circuit representation of rocks should include non-ideal elements such as frequency dependent values of R and C. Consequently, the constitutive relations (equations 1.6.1 to 1.6.3) would be, in general, functions of frequency with σ, ε, and μ frequency dependent and complex. This leads to the concept of effective EM properties which are those actually measured by experiments. The effective conductivity, σe is the parameter that relates to the component of total current density that is in-phase with the electric field and the effective dielectric permittivity, εe relates the out-of-phase current density to the electric field. The consequences of this are that the effective parameters are not the true quantities as defined in Section 1.7 but they are combinations of them. Appealing to Maxwell’s equations in the frequency domain, Fuller and Ward (1970) show the effective quantities to be
| σe(ω) = σ'(ω) + ωε''(ω), | (1.8.1) |
| εe(ω) = - σ''(ω)/ω + ε'(ω), | (1.8.2) |
and the effective dielectric constant is
| Ke(ω) = - σ''(ω)/(ωe0) + K'(ω). | (1.8.3) |
Examples of laboratory measurements of the effective dielectric constant and conductivity for various rocks as functions of rock type, water content, and frequency, are presented in Figures 1.10 and 1.11(Ward et al., 1968).
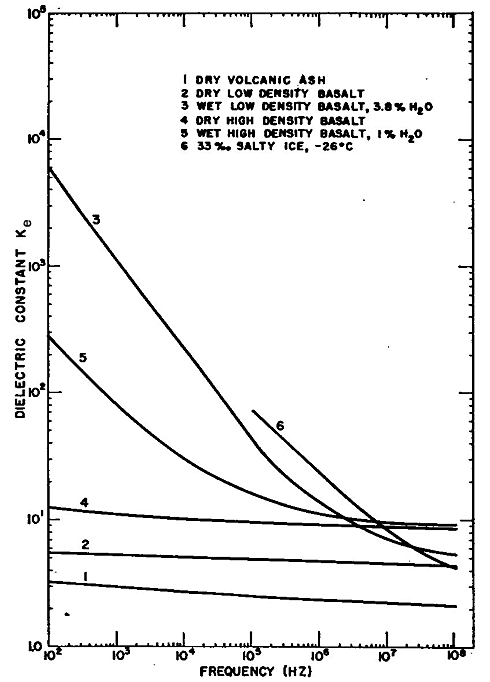 |
| Figure 1.10. Effective dielectric constant Ke versus
frequency for selected earth materials (modified from Ward et al., 1968). |
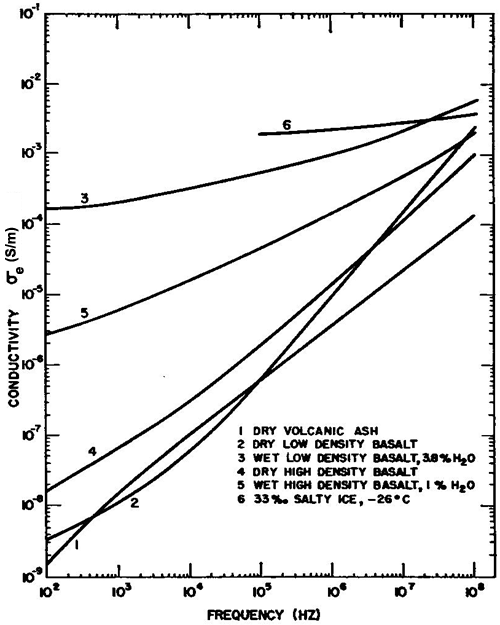 |
| Figure 1.11. Effective conductivity σe
versus frequency for selected earth materials (modified from Ward et al., 1986). |
Low Frequency Resistivity of Rocks
The low frequency (i.e., approximately zero frequency or direct current, dc) resistivity range found in natural materials spans over 20 orders of magnitude, from highly conductive ore minerals to highly insulating minerals such as micas. Figure 1.12 is a repeat of Figure 0.3 (Palacky, 1988).
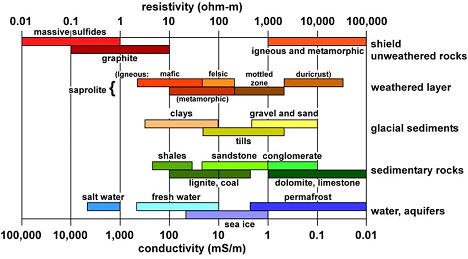 |
| Figure 1.12. Typical ranges of electrical resistivity (ohm-m) or conductivity (mS/m) for selected Earth materials (Palacky 1988).. |
Water is the most important variable in hydrologic resistivity studies because the solid rock matrix or soil grains are comparatively very good insulators (Figure 1.12). Consequently, the ions dissolved in water are the electric charge carriers responsible for the bulk material’s ability to conduct electricity. This is true for both "clean" (clay-free) and "shaly" (clay-rich) formations as will be explained below.
Factors affecting the resistivity of surficial earth materials (e.g., McNeill, 1990) are: 1) porosity, 2) texture which influences pore space interconnectivity, 3) water resistivity, 4) degree of water saturation, 5) temperature, and 6) clay content.
The first three variables are included in the
classical form of Archie’s empirical “law” (Archie,
1942) which assumes complete water-saturation
and no clay. Here, the bulk (total, t) formation resistivity, ρt is given by
| ρt = ρw a φ-m . | (1.8.4) |
where a is called the coefficient of saturation, ρw is the resistivity of the water (or electrolyte), φ is the fractional porosity, and m is usually called the cementation factor. The dimensionless constants in Archie’s equation vary with a = 0.6 to 1.0 (a = 1 is often implicitly assumed) and m = 1.4 to 2.2 (Ward, 1990). The ratio ρt /ρw, referred to as the formation factor, equals φ-m when a = 1 and is ~ 4 for common values (McNeill, 1990) such as m = 1.6 and φ = 0.4 (40 % saturated porosity).
Instead of the resistivity, its reciprocal the conductivity, is often reported instead, hence the alternate form of Archie’s law:
| σt = 1/a σwφm. | (1.8.5) |
Archie’s law (equation1.8.6 or 1.8.5) is obviously a nonlinear expression since the functional relationship, e.g., between σt and σw above, is a power function of φ. This relationship is a straight line when the log of σt versus the log of σw is plotted as is commonly done.
Archie’s law (1.8.4) has been modified to allow for any degree of water saturation, Sw (the volume ratio of the pore water to the total pore volume, factor 4 above) resulting in
| ρt = (a ρwφ-m)/ Swn | (1.8.6) |
The saturation exponent n is often assumed to
be 2. As pointed out by Ward (1990), this
equation is important in groundwater studies
since the fraction of water saturation, Sw can
be calculated if a, m, and n can be estimated
(e.g., a = 1, m = 1.6, and n = 2) and ρw, ρt,
and φ can be independently measured. The water
resistivity, ρw can be measured in the field
or in the lab; ρt can be measured by borehole
electric logs or by field measurements; and φ can be measured by borehole porosity logs, in
the laboratory, or simply estimated. Use of Archie’s
saturation equation (1.8.6) or Archie’s
law (1.8.4) makes one very big assumption and
that is that the formation is clay-free. The
effect of clay content is discussed below.
The influence of factor 5 above, namely temperature,
results in a decrease in resistivity as temperature
rises (up to a few hundred oC) since the ion
mobility in water increases. Usually this is
not significant in very near-surface studies since
the temperature coefficient of resistivity is
about 2.5% per oC (Ward, 1990). However,
it can be a substantial effect depending on the
geothermal gradient and water salinity. This
is the basis for using resistivity methods in
prospecting for water-dominated geothermal systems.
The dependency of water resistivity on salinity
and temperature is illustrated in Figure 1.13
from Nesbitt (1993).
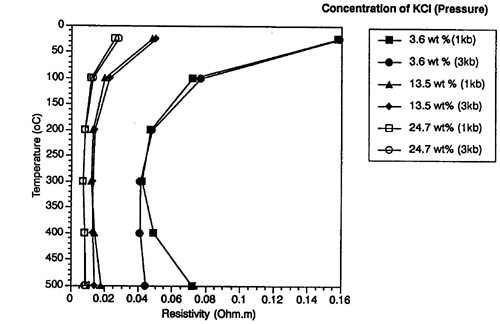 |
| Figure 1.13. Electrical
resistivity versus temperature for varying concentrations of KCl and pressures (Nesbitt, 1993). |
The effect of factor 6 above, the clay content, is the subject of numerous publications on the resistivity of clay-bearing formations. Most mathematical models use the fraction of clay present or the cation-exchange capacity of the specific clay mineral to empirically estimate the bulk formation resistivity (or conductivity). Recent nonlinear formulations of this problem use a separate clay conductivity, σs (s for shale), embedded in a host fluid of conductivity σw. This serves to emphasize that the unusually high conductivity of clay occurs only when clay particles are surrounded by water resulting in an additional form of ionic conduction. Conversely, this also emphasizes that dry clay has high resistivity.
The abnormally low resistivity of clay minerals is caused by mobile cations in the fluid that are required to balance the negative surface charge on most clay particles. Negative surface charge is caused by broken bonds on grain edges and crystal lattice substitutions on cleavage surfaces. The ion exchange capacity of a mineral is a measure of the number of cations required to neutralize this negative surface charge. Every mineral has an ion exchange capacity; clay minerals, especially montmorilllonite and vermiculite, have large values. But, because the cation exchange phenomenon is surface dependent, it is also greater for fine grain compared to coarse grain formations with identical volumes of the same clay mineral. Since both the mineralogy and grain size are important, both clay minerals and clay-size particles exhibit enhanced ion exchange capacity. In the presence of a fluid the adsorbed cations form a double layer attached to clay surfaces (Ward, 1990). One layer is immobile and fixed to the clay particles. The other layer, referred to as the diffuse layer, varies in concentration in the fluid as a decreasing function of distance from the clay surfaces. The diffuse cations are free to move under the influence of a voltage-causing electric field. These loosely bound cations effectively increase the charge density available for ionic conduction in the electrolyte. Such an additional conductivity contribution is referred to as surface conductivity or the double layer effect. It can exceed the normal water conductivity by many times and is thus of utmost importance in clay-rich zones. The effect is generally more important when the water conductivity, therefore, the intrinsic ion content, or the porosity is low. It is important to realize that when water is extracted from a formation, the conductivity measured of the sample is that of the intrinsic water conductivity, σw. It does not include any contribution from the exchange cations which remain attached to the mineral grains. Therefore, measured water conductivity values should be considered as under-estimates of the effective ionic conductivity, σe, as measured by EM geophysics when clay is present.
Mathematical expressions that include all of the six factors above have too many unknowns to permit their general, practical application. However, in some cases the local aquifer conditions can be characterized and known or estimated parameters permit application of expressions such as Archie’s relations. It is expected that the effect of clay becomes negligible in cases where the water conductivity (therefore, salinity) is large resulting in σw >> σs. Surprisingly, when the water conductivity is low, σw << σs, a form of Archie’s law (1.8.5) is appropriate. However, estimates of conductivity when σw ~ σs easily can be wrong by orders of magnitude when simply applying Archie’s relations in clay-rich environments.
A free software program called SIGMELTS (Pommier and Le Trong, 2010) is available online to calculate the bulk conductivity of two-phase Earth materials using various models including Archie's law. The program also allows discrimination of variables such as temperature, pressure, and water content.
High Frequency EM Properties of Rocks
Table 1.1 lists electromagnetic properties of various Earth materials at a frequency of 100 MHz (Davis and Annan, 1989).
 |
| Table 1.1. Dielectric constant, conductivity,
velocity and attenuation at 100 MHz for various geologic materials. |
References
Archie, G.E., 1942, The electrical resistivity log as an aid on determining some reservoir characteristics: Trans. Am. Inst. Min. Metal. Am. Petr. Eng., v.146, 54-62.
Davis, J.L. and A.P. Annan, 1989, Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy: Geophys. Prosp., 37, 531-551.
Feynman, R. P., Leighton, R. B., and Sands, M., 1963, The Feynman Lectures on Physics, vol. 1, 22.10, Addison-Wesley Pub. Co.
Fuller, B.D and Ward, S.H., 1970, Linear system description of the electrical parameters of rocks: IEEE Trans. Geosci. Elect., GE-8, 1, 7-18.
McNeill, J.D., 1990, Use of electromagnetic methods for groundwater studies, in Ward, S.H., Ed., Geotechnical and environmental geophysics, 01, Soc. Expl. Geophys., 191-218.
Nesbitt, B.E., 1993, Electric resistivities of crustal fluids: J. Geophys. Res., 98, 4301-4310.
Palacky, G. J., 1988, Resistivity characteristics of geologic targets, in Investigations in Geophysics vol. 3: Electromagnetic methods in applied geophysics-theory, vol. 1, edited by M. N. Nabighian, Soc. Expl. Geophys., 53–129.
Pommier, A., and Le Trong, E., 2010, “SIGMELTS: A web portal for electrical conductivity calculations in geosciences, Computers and Geosciences, vol. 37, 1450-1459.
Ward, S.H., 1990, Resistivity and induced polarization methods: in S. H. Ward, Ed., Geotechnical and environmental geophysics, vol. 1 – Review and tutorial, Soc. Explor. Geophys., 147-189.
Ward, S.H, Jiracek, G.R., and Linlor, W.I., 1968, Electromagnetic reflection from a plane-layered lunar model: J. Geophys. Res., 73, 1355-1372.
