1.7 Complex EM Properties
For many geophysical applications we neglect the permittivity (ε or K) term and assume the magnetic permeability is that of free space, i.e., Km = 1. This cannot be done for ground penetrating radar, GPR. In this case we must treat the total current density, JT as
| JT = JC +∂D/∂t. | (1.7.1) |
Here, JC is the same current density, J defined earlier, however, in the context here it is usually referred to as the conduction current density to distinguish it from the displacement current density, ∂D/∂t.
By assuming that the time dependency of all fields is e+iωt we see that
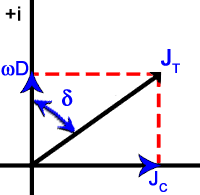
| JT = JC + iωD | (1.7.2) |
| (1.7.3) |
(Using the exponential, e+iωt to express a sinusoidal time variation with time is discussed in Appendix B). Equation 1.7.3 allows a generalized complex expression of Ohm's law (equation 1.5.1). This uses the definition of complex conductivity, σ* as
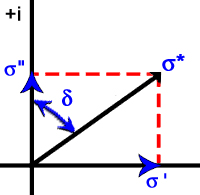
| σ* = σ' + iσ'' | (1.7.4) |
and yields
| JT = σ*E, | (1.7.5) |
where σ' = σ and σ'' = ωε are the real and imaginary parts of the complex conductivity, σ* respectively. A convenient way to express the relative amount of conduction current versus displacement current is the loss tangent, tan δ.
|
(1.7.6) |
Another way to express JT is to modify the JT equation 1.7.3 above as
| JT | = iω(σ/ iω + e)E | |
| = iω(ε - iσ/ ω)E | ||
| = iωε*E | (1.7.7) |
This leads to the definition of complex electric permittivity, ε* (von Hippel, 1954) as
| ε * = ε' – iε'' , | (1.7.8) |
where ε' and ε'' are the real and imaginary parts of the complex permittivity, ε*, respectively. This allows the alternate expression of the loss tangent to be
| tan δ = ε'' / ε' | (1.7.9) |
The complex dielectric constant, K* follows as
| K* | = ε*/ε0 | |
| = K' – iK''. | (1.7.10) |
Davis and Annan (1989) prefer to separate the imaginary part of the dielectric constant into two parts: 1) a dc component of conductivity σdc and 2) a high frequency contribution, K''. Then
| K* | = K' – iK''' | |
| = K' + i(K'' + σdc/ωε0) | (1.7.11) |
The relations above can be represented in the complex plane. Figure 1.9 a, b, and c contain such examples.
a) |
b) |
c) |
 |
 |
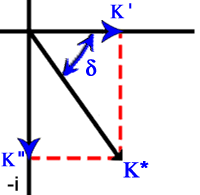 |
Figure 1.9 Complex graphical representations of a) total current density, JT, b) conductivity, σ*, and c) dielectric constant, K*. |
||
