1.2 Series RLC Circuit

 

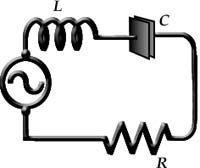Figure 1.2. Series RLC circuit.

A time-varying voltage, V(t) (assumed for simplicity to be sinusoidal), applied to a series RLC circuit, causes a sinusoidal current to flow given by

I(t) = I0 sin ωt

(1.2.1)

where ω = 2πf is angular frequency, f = 1/T is the harmonic frequency with period T. The instantaneous current through each circuit element is the same. This is referred to as being in-phase and since the current is in-phase in each circuit element, it is a good phase reference.

Series RLC Current-Voltage Relationships

Across the resistor, Ohm's law says that there is a linear relationship between current and voltage, V_R, i.e.,

VR = IR,

(1.2.2)

where the resistance, R is the constant of linear proportionality.

Across the inductor, Faraday's law says that a voltage, V_L, that is induced is proportional to the time rate of change of magnetic flux. This is expressed using the change in current flow, dI/dt as

VL = L dI/dt,

(1.2.3)

where the inductance, L is the constant of linear proportionality.

Across the capacitor, the voltage depends on the capacity to store electric charge. The ratio of the charge, q to the voltage (potential difference) across such a device defines capacitance, C such that

VC = q/C.

(1.2.4)

Applying Kirchhoff's voltage (second) law (the sum of the voltage drops in a closed loop equals the source voltage) yields

V = VR + VL + VC

(1.2.5)

or

V = IR + L dI/dt + q/C.

(1.2.6)

Using

I = I0 sin ωt

(1.2.7)

and recalling that the definition of current is

I = dq/dt,

(1.2.8)

we find after integration that

q = -(I0/ω) cos ωt.

(1.2.9)

Whereupon, after substitution into equation 1.2.6 above yields

V = I0R sin ωt + I0ωL cos ωt - (I0/ωC) cos ωt.

(1.2.10)

The quanities ωL and 1/(ωC) are the impedances of L and C which are called the inductive reactance, X_L and capacitive reactance, X_C , respectively. They clearly must have the units of ohms like R.

Figure 1.3. A oscilloscope can measure current and voltage time variations.

Imagine placing a device that can record the time variations of the voltages with respect to the current variation through the circuit element. Such a device is an oscilloscope (Figure 1.3). Using the current for the phase reference one can now compare the temporal phase relations between I, V_R , V_L , and V_C (Figure 1.4).

Figure 1.4. Temporal current and voltage relations across series RLC circuit elements.